GATE-CH-1997-27-ctrl-5mark
1997-27-ctrl
A control system is shown below.
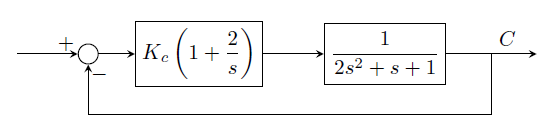
Using the Routh test, determine the value of \(K_c\), at which the system just becomes unstable.
0800-1-ctrl
The characteristic equation of a process is: \[ C = \frac{G_1G_2}{1+G_1G_2H}R + \frac{G_2}{1+G_1G_2H}U\] The open-loop transfer function is:
1995-1-r-ctrl
The root locus method, a pole of a transfer function \(G(s)\) is the value of \(s\) for which \(G(s)\) approaches:
1997-1-25-ctrl
The open-loop transfer function of a process is \(K\dfrac {(s+1)(s+4)}{(s+2)(s+3)}\). In the root locus diagram, the poles will be at
1998-1-23-ctrl
The Root locus plot of the roots of the characteristic equation of a closed loop system having the open loop transfer function \[ \frac {K(s+1)}{s(2s+1)(3s+1)} \] will have a definite number of loci for variation of \(K\) from 0 to \(\infty \). The number of loci is
2010-5-ctrl
| GROUP I | GROUP II |
|---|---|
| P. Pole in the right half plane | I. Stable response |
| Q. Pole at origin | II. Integrating response |
| R. Zero in the right half plane | III. Unstable response |
| IV. Inverse response |
2014-9-ctrl
1993-26-b-ctrl
A closed loop feedback control system consists of a second order process \[ G_p(s) = \frac {K_p}{(\tau _1s + 1) (\tau _2s + 1)} \] and a proportional controller \(G_c(s) = K_c\). The roots of characteristic equation of the closed loop system are \(-2\) and \(-1\) in absence of controller and roots are \(-1.5 \pm 0.5i\) when \(K_c = 4\).
(A) Determine (i) \(K_p\), (ii) \(\tau _1\), (iii) \(\tau _2\).
(i) \(K_p\)
{#1}
(ii) \(\tau _1\)
{#2}
(ii) \(\tau _1\)
{#3}
(B) Determine the maximum value of \(K_c\) so that the response of the system to a step input is non-oscillatory.
{#4}
1994-28-ctrl
The characteristic equation of a closed loop control system is \[s^4 + 4 s^3 + 6 s^2 + 2 s + 3 = 0 \] The system is
1999-2-17-ctrl
Which of the systems having the following transfer functions is stable?
2005-47-ctrl
2009-42-ctrl
1997-27-ctrl
A control system is shown below.

Using the Routh test, determine the value of \(K_c\), at which the system just becomes unstable.
1998-24-ctrl
The characteristic equation of a closed loop control system is \[0.25 s^3 + 0.8 s^2 + 5.6 s + 1 + 0.35 K = 0 \] Find the limiting value of \(K\), above which the closed loop system will be unstable.
IN-2014-50-ctrl
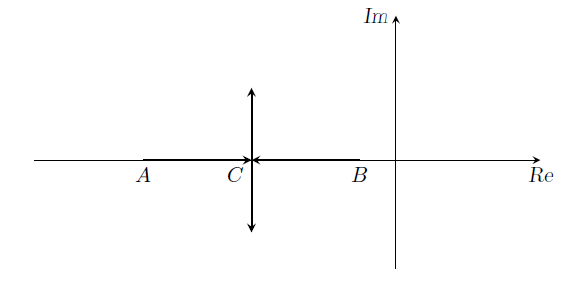
1995-29-ctrl
The transfer function of a process, measuring device, controller and control valve, respectively is given by \[ G_p = \frac {K_p}{(s+1)(s+4)}; \quad \quad G_m=1; \quad \quad G_c=K_c; \quad \quad G_v=1 \] The root locus diagram of the system is given in figure.
Last Modified on: 02-May-2024
Chemical Engineering Learning Resources - msubbu
e-mail: learn[AT]msubbu.academy
www.msubbu.in