Variable area meters - Rotameter

Home -> Lecture Notes -> Fluid Mechanics -> Unit-III

In the variable head meters the area of constriction or orifice is constant and the drop in pressure is dependent on the rate of flow. In the variable area meter, the drop in pressure is constant and the flow rate is a function of the area of constriction.

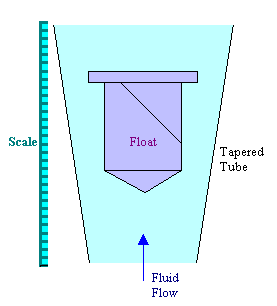
A typical meter of this kind, which is commonly known as rotameter consists of a tapered glass tube with the smallest diameter at the bottom. The tube contains a freely moving float which rests on a stop at the base of the tube. When the fluid is flowing the float rises until its weight is balanced by the upthrust of the fluid, the float reaches a position of equilibrium, its position then indicating the rate of flow. The flow rate can be read from the adjacent scale, which is often etched on the glass tube. The float is often stabilized by helical grooves incised into it, which introduce rotation - hence the name. Other shapes of the floats - including spheres in the smaller instruments may be employed.

The pressure drop across the float is equal to its weight divided by its maximum cross-sectional area in the horizontal plane. The area for flow is the annulus formed between the float and the wall of the tube.

This meter may thus be considered as an orifice meter with a variable aperture, and the formula derived for orifice meter / venturi meter are applicable with only minor changes.

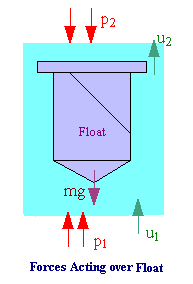
Both in the orifice-type meter and in the rotameter the pressure drop arises from the conversion of pressure energy to kinetic energy (recall Bernoulli's equation) and from frictional losses which are accounted for in the coefficient of discharge.

Dp/(rg) = u₂²/(2g) - u₁²/(2g) à 1

Continuity equation:

A₁u₁ = A₂u₂ à 2

Where A₁ is the tube cross-section, and A₂ is the cross-section of annulus (area between the tube and float)

From equn.1 and 2,

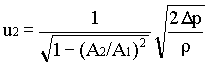à 3

The pressure drop over the float Dp, is given by:

Dp = V_f(r_f - r)g / A_f à 4

where V_f is the volume of the float, r_f the density of the material of the float, and A_f is the maximum cross sectional area of the float in a horizontal plane.

Substituting for Dp from equn.4 in equn.3, and for the flow rate the equation is arrived as

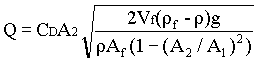
The coefficient C_D depends on the shape of the float and the Reynolds number (based on the velocity in the annulus and the mean hydraulic diameter of the annulus) for the annular space of area A₂.

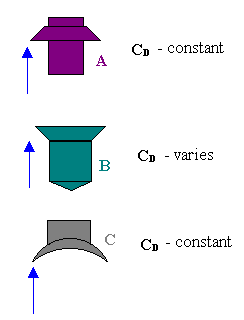
In general, floats which give the most nearly constant coefficient are of such a shape that they set up eddy currents and give low values of C_D.

The constant coefficient for the float C arises from turbulence promotion, and for this reason the coefficient is also substantially independent of the fluid viscosity. The meter can be made relatively insensitive to changes in the density of the fluid by the selection of the density of float, r_f. If the density of the float is twice that of the fluid, then the position of the float for a given float is independent of the fluid density.

Because of variable-area flowmeter relies on gravity, it must be installed vertically (with the flowtube perpendicular to the floor).

The range of a meter can be increased by the use of floats of different densities. For high pressure work the glass tube is replaced by a metal tube. When a metal tube is used or when the liquid is very dark or dirty an external indicator is required.

The advantage of rotameters are direct visual readings, wide range, nearly linear scale, and constant (and small) head loss. It requires no straight pipe runs before and after the meter.